Research

High Performance Parallel Sparse Tensor Computations

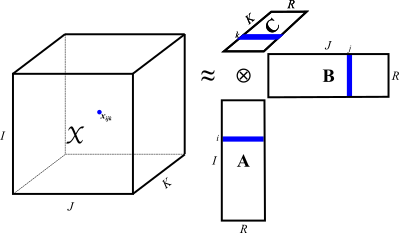Tensor factorizations are widely used in the literature to model, approximate, and compress high dimensional data for which low-rank assumptions hold. Many high dimensional real-world data can naturally be expressed as sparse tensors; thereby can be analyzed using tensor factorization.

I am particularly interested in providing high performance parallel sparse tensor factorization kernels to scale such analysis to thousands of processors. I focus on shared and distributed memory parallel algorithms, tensor data structures for computational and memory efficiency, computational techniques to reduce the amount of computations, and tiling, reordering, partitioning strategies to improve efficiency and scalability of our implementations. In our recent work, we parallalized CANDECOMP/PARAFAC (CP) and Tucker decomposition algorithms, and achieved up to 700x speedup using 2048 cores. We implemented these algorithms in our templated C++ library HyperTensor, which uses OpenMP and MPI for shared and distributed memory parallelism (will be available soon).

Graph and Hypergraph Algorithms

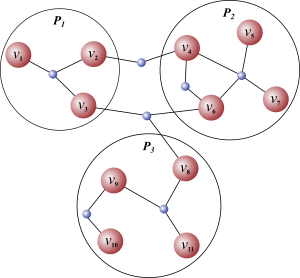Graph and hypergraph algorithms and tools are extensively used in combinatorial scientific computing to accelerate computational methods in various ways. In my research, I am particularly interested in casting outstanding algorithmic challenges to existing graph and hypergraph problems for which efficient solutions exist, or introducing new problems together with exact algorithms or effective heuristics for their solution, and complexity analysis. For instance, in our recent work, we introduced the problem of covering or partitioning the edges of a graph by the minimum number of quasi-cliques with some fast heuristic solutions, and demonstrated that the problem is NP-Hard. Using these heuristics, we performed graph-to-hypergraph transformations over the adjacency graph of a matrix using quasi-clique cover, then executed a particular hypergraph partitioning algorithm to better minimize the fill-in for sparse direct solvers.

I also investigate graph and hypergraph models of numerical methods to capture their computation, communication, and memory costs; then benefit from the existing graph or hypergraph partitioning software to improve their performance. In our recent work, using the hypergraph partitioning models of parallel tensor factorization, we were able to reduce the communication volume by 20x and achieve 5x more parallel speedup, only by rearranging the data/task assignments of the computational kernels we implemented.